3D打印网-中国3D打印门户移动版

 工艺-性能-使役性能的联系

从技术和经济上的观点来看，过程参数的选择对优化AM性能是必需的。在工艺、性能和使役性能之间建立直接联系是科学家和工程师非常感兴趣的。这种联系通常是高度非线性的，因为输入变量的数量通常大于3个。因此，很难确定这种联系的基础数学公式。由于NN模型固有的非线性特性，它已被应用于为各种AM过程建立这些数学关系。表1总结了NN在AM中的应用（实际上，NN在这里称为MLP，因为所有数据集都是表格类型），并列出了作为输入的工艺参数值和作为输出的性能/使役性能。从表1中可以看出，不同的AM技术应该选择不同的输入特征，因为确定AM部件的关键因素是不同的。此外，由于大量参数会对最终成品产生影响，所以确定选择哪些参数需要深入了解AM过程。

表1 NN应用程序，用于构建过程-性质-性能联系

SL: stereolithography; LMD: laser metal deposition; WAAM: wire and arc additive manufacturing

NN算法的详细设置总结在表2中。确定NN结构的典型超参数通常由4部分组成：隐藏层数目、单层中神经元数量、激活函数和损失函数。

表2 有关NN算法的详细信息

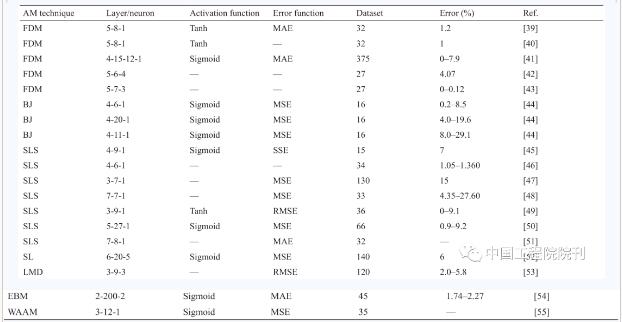MAE: mean absolute error; RMSE: root mean square error; SSE: sum square error

（1）隐藏层数目。在表2的“Layer/neuron”列中，“5-8-1”表示该NN结构包含3层：输入层有5个神经元，唯一的隐藏层有8个神经元，输出层有一个神经元。从表中可以看出，一个隐藏层足以应对大多数AM问题。

（2）单层神经元数量。输入层和输出层的神经元数由问题本身决定。然而，需要仔细选择唯一隐藏层的神经元数量，因为它与ML中的欠拟合和过拟合问题直接相关。根据表2，我们建议至少以5~10个神经元作为隐藏层神经元的最佳数量。

（3）激活函数。激活函数是输入信号的非线性变换，它决定是否应该激活神经元。这对NN至关重要，因为没有激活函数的网络只是一个线性回归模型，无法处理复杂的任务。一些流行的激活函数类型如下：

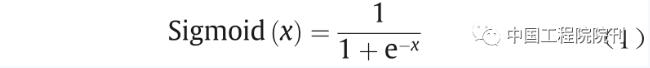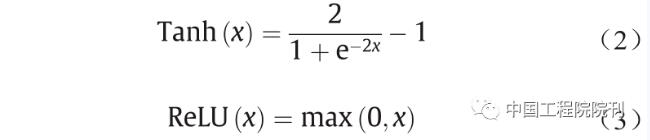
在实际应用过程中，sigmoid和tanh函数的任一侧以及ReLU函数负轴的梯度将会很小，甚至趋于零，因此，在学习期间权重无法得到更新调节。这种情况就是典型的梯度消失问题。使用Max-min归一化技术将输入特征的范围变更为(0, 1)，其可以有效地避免这个问题。如有必要，还可使用批标准化技术，以便继续细化每一层的输入信号。

（4）损失函数。损失函数应由确切的问题确定，并且通常带有实际的解释。例如，均方根误差（RMSE）和平均绝对误差（MAE）都是评估预测值和目标值两个向量之间距离的方法。其表达方式如下：

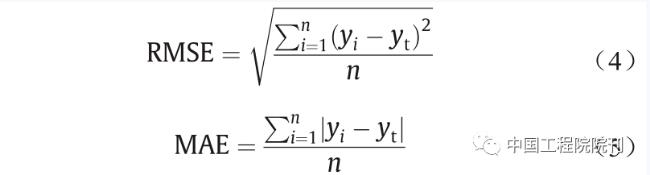
式中，i 是样本索引；yi 是预测值；yt 是目标值。它们之间存在一些小的变化：计算RMSE对应于L2范数（即欧几里德范数），这是最常见的欧式距离；计算MAE对应于L1范数（即曼哈顿范数），其测量从原点到目标的矩形网格中的距离。一般来说，Lp规范由下式表示：

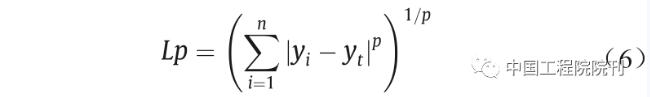
式中，p是范数指数。p值越大，则它对较大的值越敏感。例如，由于L2范数使误差平方，因此模型将产生比L1范数大得多的误差。如果这种情况是一个异常值，L2范数将更加关注这个单一的异常情况，因为许多其他常见情况的误差较小。换句话说，如果考虑每个异常值都很重要的话，RMSE方法是更好的选择。反之则MAE适用于可以安全有效地忽略异常值的情形。应当注意的是，在某些特殊情况下，可能有必要考虑自定义设计损失函数。

挑战和可能的解决方案

(责任编辑：admin)